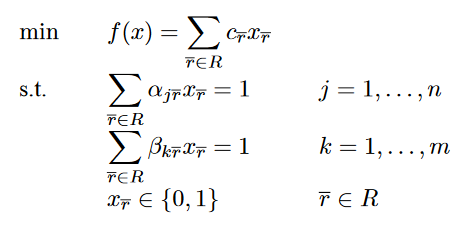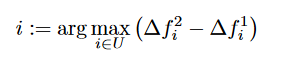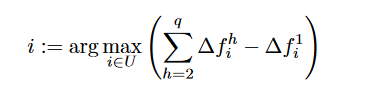Adaptive Large Neighborbood Search
Adaptive Large Neighborhood Search
假设下面的场景,有M个点的L量的货物,在规定的时间窗内,由K辆车运输到N个客户手中,并且满足货物的一些特殊约束。那么需要求出一组线路,使得这些线路的综合成本最低,这在物流领域是非常常见的一个问题。从数学的角度来分析,这是一个约束满足问题(CSP-Constraint Satisfaction Problem),也是一个组合优化的问题。从业务类型的角度来分析,又可以分成下面几种主要的场景
- VRPTW,带有时间窗的车辆线路优化
- CVRP,限制装载量的线路优化
- MDVRP,多基地配送线路优化问题
- SDVRP,站点独立线路优化,实际上是指每个服务点,都有自己的需求,一般是指配送商品需要一些特殊的车辆才能配送
- OVRP,开放车辆线路优化问题,不需要返回基地,线路的开放是相对于闭环而言的
- VRPB, 需要返回取货,例如配送完成之后,回收一些容器
rich pickup and delivery problem with time windows
所有的这五类问题,都可以被转换为 RPDPTW(rich pickup and delivery problem with time windows)并且通过 Adaptive Large Neighborhood Search 框架来解决
公式定义
拥有 n 个 request 和 m 个 vehicle,在一个图上定义,则是 P = { 1,2,...., n },是 pickup 节点,D = { n + 1, .... ,2n },是 delivery 节点。request i 通过 节点 i 和 i+n 表示。K = {1,.... ,m} 代表vehicle,vehicle和request的绑定关系为Pk 包含于 P并且Dk 包含于 D,表示一组pickup任务Pk和一组deliver任务Dk被vehicle k运输。每一个request必须被同一个vehicle服务,因此假设i 属于 Pk 推导出 i+n 属于 Dk反之亦然。
定义N = P 并上 D 并且 Nk = Pk 并上 Dk,让Tk = 2n + k,k 属于 K,并且Tk' = 2n + m + k ,k 属于 K,分别代表vehicle k的起点和终点。
有向图 G = (V , A) 由点 V = N 并上 { T1,.... Tm } 并上 {T1',....Tm'}以及边A = V * V构成。
每一个vehicle k有一个子图 Gk = (Vk, Ak),子图Vk = Nk 并上 {Tk} 并上 {Tk'} 以及 Ak = Vk * Vk,对每条边(i,j) 属于 A 设其距离为 d(i,j) >= 0时间为t(ij) >=0并且假设行驶时间满足三角不等式如果i,j,k 属于 V则有t(i,j) <= t(i,l) + t(l,j),对于任意i 属于 V设服务时间为s(i),服务时间窗为[a(i),b(j)],对于i 属于 N定义l(i)为该点需要装载到vehicle中的货物数量,对于i 属于 P 有l(i) >= 0对于i 属于 D有 l(i) = -l(i-n),每一辆车的装载限制为Ck,每一个节点都会被赋予次序Πi,次序较低的点,会在次序较高的点之前被访问。
每一个vehicle都会有一条合法的线路,从起点Tk到终点Tk'
r = (Tk = v1, v2,....,vh = Tk')`
并且满足服务次序,时间窗要求,车辆容量、pickup发生在deliver之前,一个request只会被vehicke k承载。我们要求vehicle只能访问被服务的节点
v(i) 属于 Nk i = 2,....,h-1
一个pickup - delivery对需要被同一辆车服务,并且pickup需要发生在delivery之前
i <= j, v(i) 属于 Pk,v(j) 属于 Dk,v(j) = v(i) + n
次序应该满足
i <= j, Πv(i) <= Πv(j)
时间窗限制,Si 属于 正实数 R+ 表示当一个vehicle开始对v(i)进行服务,我们可以得到下面的限制约束
a(i) <= Si <= b(i) i = 1,....,h Si+1 >= Si + s(i) + t(i,i+1) a(Tk) <= S1 <= b(Tk) a(Tk') <= Sh <= b(Tk')
[a(Tk),b(Tk)]和[a(Tk'),b(Tk')]分别为起点Tk和终点Tk'的时间窗限制
装载量限制,Li 属于 正实数 R+,表示vehicle在i点装载完货物之后的装载量
Li <= Ck i = 1,....h Li+1 = Li + l(i+1) i = 1,....,h-1 L1 = 0 Lh = 0
线路r的成本为
c(r) = ∑(i=1,h-1) d(i,i+1)
可能有部分request 没有办法找到合适的vehicle,为了处理这种情况创建n个虚拟线路,虚拟线路由单个request组成,这些临时线路,不使用任何vehicle,并且有非常高的行驶成本Γ,request找不到合适的车辆,我们称之为被分配到request bank
整个问题可以描述为:R代表所有可用线路的集合,矩阵matrix(α(j,r)) r 属于 R 并且 j = 1,....n 用于确定request i 是否在线路r上,举证matrix(β(k,r)) r 属于 R 并且 k = 1,....m 用于确定线路r是否使用vehicle k。并且使用x(r)用于确定线路r是否最后的解决方案
目标函数是:所有加入到最后解决方案的线路的成本总和最低。
虚拟线路没有被分配任何车辆,因此对于虚拟线路r,我们有β(k,r) = 0 , k = 1,....,m
问题转换
VRPTW 转换为 RPDPTW
将每一个customer映射为一个request,request从depot中pickup,并且delivery到customer所在的点。pickup的时间窗为[a(d),a(d)],其中a(d)是从depot离开的时间窗,serviceTime为0,delivery的时间窗则是customer保持一致。顺序方面,为了把线路设计为从depot装货,配送到其他的点,而不是配送一个点后完后重新回来装载。将所有的pickup优先级设置为0,所有的delivery优先级设置为1,这样vehicle就会优先将所有的pickup任务先完成,然后再去配送pickup对应的delivery任务,之后再返回到depot中。
MDVRP 转换为 RPDPTW
在使用MDVRP,会有多个depot用于服务,在RPDPTW中,必须有一个depot用于pickup,而在MDVRP并不清楚request会被哪一个depot服务。
为此,我们创建一个虚拟基地base,所有的线路都从这里出发,并回到这里,所有正常的request的pickup都在这里。同时为每一个vehicle创建一个虚拟request。对于虚拟request的pickup和delivery地点则和对应的vehicle地点一致。虚拟request的数量要求为00,也没有任何servicetime,可以在任意时间窗被服务。设对于每一个vehicle都有Nk包含了对应该vehicle的虚拟request和其他正常的request。
优先级上,正常的request为pickup和delivery分别设置优先级为 0 和 2,对于虚拟request则设置为 1 和 3,这保证了所有的正常request的delivery被对应虚拟reuqest的pickup和delivery包围起来。正常request的pickup节点到到其他所有的节点,距离和时间都设置为 0 ,其他的距离和时间则使用默认的距离和时间。
在这个转换方式中,RPDPTW中,每一条线路都会从虚拟的base中出发,执行pickup节点的任务,然后执行对应虚拟request的pickup任务,最后执行其他正常request的delivery任务,最后执行虚拟request的dellivery,最后回到线路的终点。从虚拟request的pickup之前,到正常request的delivery之后,所有的距离和行驶时间都是 0 。 对于前面提到的虚拟线路,我们需要设置一个非常高的成本,避免虚拟request被加入到request bank中。
ALNS
ALNS是一个局部搜索框架,由一系列简单的算法一同修改问题的解。在每一次迭代算法中,会选择一个算法修改当前解,并选择一个算法用于修复当前解,修改和修复的概念和之前提到的Ruin&Recreate是一样的。如果得到的新解能够满足约束条件,则被接受。
VNS 可变领域搜索,先使用小的启发式搜索算法改进当前解,如果陷入了局部最优陷阱,使用大的启发式搜索改进当前解。和ALNS相比,ALNS的自适应层能够根据变量选则不同的启发算法
min {f(x) : Ax <= b, x 属于 自然数}
简述ALNS算法框架
ALNS基于局部搜索框架,例如SA、禁忌搜索等。 在循环中的每一次迭代,会使用适配层(adaptive layer),根据之前每一个算法(每一个算法会产生一个领域解,这个解对比之前的解的改善)的得分(score),从其中随机地(轮盘赌算法)选择一个用于destory和一个用于repair的算法。如果一个算法,改善的解更多,那么他的得分也越多。因此他越可能被选择。第j个领域被选择的概率为
` πj / ∑(i=1,m) πi , 一个m 个领域,每一个领域的得分为 πi`
destory领域和repair领域的选择是完全独立的,分别使用不同的赌盘算法完成
对于大多数情况,我们使用的启发式算法都是速度比较快的,如果有一些算法明显慢于其他的算法,那么在计算得分π的时候,需要进行标准化,以便在时间和解的质量上得到一个正确的平衡。
在第四行中,我们使用N-中选择的destory算法对当前解x进行破坏,使用从N+中选择的repair算法对破坏后的解进行修复。在destory和repair算法这种,适当选择一些噪声或者随机干扰,防止陷入局部最优陷阱。
在第六行中,对解进行评估之后,将每一种算法的贡献值作为分数给到每一个算法。一个更优的算法,自然会获得更高的分数。每一个destory&repair会涉及到两个算法,分数会被平均分给两个算法。
每进行M轮迭代之后,每一个算法的得分π都会被重置,之前各个算法得到的分数,可以被作为初始权重,影响之后的算法选择。
设计 ALNS 算法
- 选择一系列快速的启发式
repair算法,可用于构建局部解 - 选择一系列的
destory启发式算法,可以生成repair算法可以应用的局部解 - 选择一个本地搜多框架,作用在全局范围
desotry算法需要移除一些点,移除这些点的目的,是希望能够给后面的领域搜索,带来增强和多样性。使用的算法有
random removal随机移除worest removal移除对全局成本影响最大的点(例如减少这个点之后,得到的局部解成本降低最多)related removal有时候会选择几个点,使得他们相互调换后更容易得到一个可行解。在关联矩阵A中,每一个元素r(i,j)标识变量x(i)和x(j)对应的偏差系数,r(i,j)越小,代表对应的两个变量相关性越强。具体的r(i,j)大小需要根据具体的问题进行定义。small removal大致的原理和related removal类型,选择出偏差系数较小的点,使得他们大致能够满足约束,利于变换得到下一个有效解。history based removal基于历史记录的移除方法,统计点或者一系列点,如果这些点可能导致一个糟糕的解,则在下次移除的时候避免移除这些点
recreate 算法,需要基于具体的问题进行选择,一般是贪心算法的变体。例如最简单的每步最优、将所有的点都装载到超过其装载能力上界,然后再逐个减少代价最大的变量,直到得到一个可行解。一般ALNS使用简单的启发式算法,但是也有一些例如分支定界算法等,虽然耗时更多,但可以显著地提高解的质量,我们也会采用。
一些优化问题,可以被分解成为若干个子问题,每一个子问题可以被单独解决。我们需要考虑这些子问题,是否被逐个考虑(串行计算)或者各个子问题被同时计算(并行计算),串行启发式算法比较容易实现,但是串行启发式,可能导致最后的子问题索要处理的变量,并不适合放在一起,这可以在某种程度上通过并行启发式来得到解决。
另一个拓展优化是,对于每一个destory算法Ni-,定义一系列Ki 属于 {N+}的repair算法与之对应。如果确定了Ni-作为destory算法后,赌盘算法在选择repair算法的时候,需要再Ki中选中。
ALNS框架的特点
对于大多数优化问题,我们已经知道一些表现良好的启发式算法,这些构成ALNS算法的核心。因为算法的多样性,使得ALNS可以在更大的范围内搜索解,因此最后的结果可以更具鲁棒性,能适应具有不同特点的例子,并且很少陷入局部最优解陷阱。
ALNS 也适用于有严格约束的问题,在这类问题中,小的变换算法,很难脱离局部最优化或者难于找到一个符合各个条件的解。ALNS可以使用大规模的变换,改变更多的变量,从而找到一个可行解。
ALNS的校准,大部分取决于adaptive层;对于具体算法的校准,需要针对不同的算法单独设计更加精巧的参数。 ALNS算法的最大优点在于组合多种算法,协同工作。
ALNS应用在RPDPTW 在前面分别描述了ALNS算法和RPDPTW的核心概念模型,要使用ALNS来解决RPDPTW问题,需要将两者之间的概念进行映射 概念对应
在 ALNS 中的variables 对应RPDPTW中的request,修改变量也就是调整request的位置destory算法,对应是将request q从一个线路route中移除到request bank中repair算法,对应将request从request bank中取出并插入到合法的route中
Request Removal
要将一个request移除,我们将使用一系列不同的启发式算法,这些启发式算法都有一个特征,接受一个解x 输出 q 个 request,这些request 已经被从x中移除。
Random removal
随机选择 q 个request,并从解中移除。主要的特点是可以多样化局部搜索过程,缺点是没有目的性。
Worst removal
目的是选择最值得的request,从解中移除。在RPDPTW中,最合理的就是那些代价最高,并且插入到其他地方,会获得一个更好(代价更低)的解的rquest。 假设一个request i 在解x中,我们定义其代价为∆f-i 表示:将request i 从解 x 中完全移除前后,x 的总代价的差值。worst removal会一直指定到获取 q 个代价最高的 request为止,如果q 很大,那么一些代价没有那么高的request也会被移除。
worst removal 显然是一个贪心算法,从一个解中移除,并不代表其一定会找到一个更加合理的位置放置。
Related removal
related removal 是一组一组 request,这些request 从某种角度上来看是有关联的,从而这些request也可以互相交换。对RPDPTW,我们定义关系系统 r(i,j)标识两个request之间的距离相似度。每一个request i 可以分成 pickup node i 和delivery node i+n,因此可以得到这样的表达式
r(i,j) = 1/D ( d'(i,j) + d'(i,j+n) + d'(i+n,j) + d'(i+n,j+n) )
d’(u,v) 的计算忽略了从终点出发的距离,因为从终点(起点)可以在任何情况下访问,因此对两个request的关联系数没有贡献值。
D 表示在 后面四个 d’(u,v) 中值不为空的数量,也就是d’(u,v) 其实上是一个平均值,如果两个request都从终点(起点)提货,那么两个request之间的距离关联系数就是 d’(i+n,j+n)
Related removal 算法一般选择一个随机的request 开始,然后基于这个request,选择和其关联度最高的q 个 request移除。
Cluster removal
cluster removal 是 related removal 的变种,如果我们把线路 route 在地图上分成不同的组,我们在移除rquest的时候,最好是将整个分组都移除掉。这个是显而易见的。否则在我们执行repair的之后,很可能会将这些request返回到原地。cluster 可以基于 related removal 算法实现,这边可以了解一下 Kruskal 算法和最小生成树算法。two connected components remain不太理解意思。如果得到的request 数量小于 q,则从cluster中随机算账一个 request,从其他的线路中选择一个接近这个request的 request,添加到cluster中。
Time-oriented removal
这是related removal的另一种变体,在time oriented removal算法中,我们尝试选出在服务时间上大致相同的reqeust,也是为了便于交换。
随机选择 reuqest i 则另一个 request j ,i和j的在时间上的关联度可以表示为
t(pi) 和 t(di) 表示 request i 在当前解中的 pickup 和delivery 时间。同样地,也会获取q 个关联度最高的 reqeust
使用基于时间的移除法,一般会先从所有的request中选择一组地理上比较接近的request 子集,在这个子集中进行 time oriented removal,因为如果只考虑时间接近的话,一般在一条线路中,只有一两个request可以被选中,这很难对全局解有比较大的改进。
Historical node-pair removal
和禁忌搜索类似,历史优化记录,会对后续的removal操作带来影响。对每一组 node 对
(u,v) 属于 A,和f(u,v) 关联,f(u,v)代表目前最好的解中边(u,v)的权重,初始化的时候设置f(u,v)为无限大,每一次通过ALNS获取一个新的解的时候,都要更新A中所有边的f(u,v),一般来说这些边的权重会逐渐改善。
如果要移除 request,Historical node-pair remvoal 会计算 request(i,i+n) 的 cost,通过对所有 通过 i 和 i+n 的边计算 f*(u,v) 权重。并将权重最大的前 q 个request 移除
Historical request-pair removal
和Historical node-pair removal 类似,定义权重 h(a,b),标识两个request a 和 b 曾经被放在同一辆车上的次数。h(a,b) 初始化的时候为 0,每一次一个新的解被得出的时候,给这个权重增加计数。移除的时候,也是类似地,移除和对应的rquest关联度最高的 q 个reqeust
Inserting Reqeusts
将remove 出来尚未分配的reqeust 记为 U
Basic greedy
最简单的贪心算法,将request插入到插入后代价最低的线路
设∆f(i,k) 为将request i 插入到 线路 k 中最佳位置,带来的目标函数成本增加。如果 i 无法插入到线路 k 中,那么设置 ∆f(i,k) = ∞ ,因此我们使用贪心策略
每次从U中选择插入到线路中可能带来最小成本增加的reqeust,插入算法反复执行,直到所有的request都插入到合适的route中,每一个插入都会改变一条线路。
Regret
使用典型贪心算法的缺点是,经常会将优化难度大的request,放到最后一轮迭代中来处理,这个是时候已经没有足够的优化空间。regret 算法尝试通过一些预测信息,来进行insert 操作。
设∆f(q,i) 表示将reqeust i 插入到第 q 好的线路,增加的代价,例如∆f(2,i) 表示将 request i 插入到 第二 好的线路中增加的代价。在每一次迭代中我们选择
也就是我们每次选择reqeust进行插入的时候,都是选择第二好的选择和最好的选择差距最大的reqeust,这个差值越大的reqeust,越早被处理结果一般越好。
regret 算法也可以自然地被拓展为下面的形式
显然basic greedy算法就是 regret-1 算法,第二种则为 regret-2 算法
Master local search framework
模拟退火算法
当一个轮迭代之后会产生一个新的解,怎么判断是否接受这个解是否被接受?假设候选解是 x’ 当前 解释 x,则接受 x’ 的概率为
T > 0 是 温度,我们使用标准系数,定义冷却率 c。初始温度 T(start) 并根据T = T * c ; 0 < c <1来逐渐减少T。在选定一个初始解之后,后面的解如果和当前解相差不超过百分之 w,则有 0.5 的概率被采用,而之后,采用上述的公式进行递减
Applying noise to the objective function
为了扩大算法的搜索范围,一般需要在算法中加入一些随机的影响因素。仅仅使用模拟退火算法,显然是不够的。
因此我们在insert和removal算法中,增加一些随机因素,当计算将一个request加入到route中带来的成本增加的时候,使用 C' = max {0, C+ δ},δ就是噪声,δ的取值范围为 [-Nmax , Nmax],Nmax = η * max{d(i,j) i,j 属于 V},η是一个参数入参,我们使用线路中最长两个点的距离,定义噪音的对最终目标函数的影响程度。
而是否引入噪音影响,也可以使用赌盘算法。
调整算法权重
ALNS 框架中Adaptive的特性体现在其能够根据算法运行的过程,动态地调整每一个启发式算法的使用。这取决于每一种算法所得到的分数πi。
这些分数在若干次迭代段(segment,一般100次迭代,定义为一个段)中收集。分数π’(i,j)表示算法i 在第 j 段中的得分。那些解会导致对应的算法增加分数
- 操作,产生一个新的全局最优解
- 操作,产生一个新的解,并且有当前解
- 操作,产生一个新的解,这个虽然没有当前解好,但是仍然被接受
后面两种情况主要是为了鼓励拓展搜索的范围。每一段segment迭代结束之后,计算分数
ai 表示对应算法在这次segment中被调用的次数,ρ控制调整权重的速度,如果ρ = 1 ,则轮盘算法全部根据最近一次的 segment的结果来进行判断,如果ρ <1 则会将之前的值加入考虑。
最小车辆使用
在目前的描述中,都是为了最小化车辆的行驶距离,为了最小化车辆数,我们使用两阶段策略。
使用启发式算法得到一个 m 辆车构成的解,我们从其中移除一个线路,并将全部的request都移到 request bank中,如果ALNS 还能够找到一个解,我们设置一个大的代价Γ用于鼓励这个解。
如果没有找到,则回到原来的可行解。
Epilog
本文主要参考《A general heuristic for vehicle routing problems》可以视为其的一个读后总结。